Программирование циклических вычислительных процессов

Цель: Приобрести навыки программирования циклических вычислительных процессов.

Теоретические разделы для выполнения лабораторной работы

1. Организация циклических процессов при решении вычислительныхзадач.

Задание к работе

А) Вычислить значение выражения (по вариантам, см. приложение 2) в цикле x Є [x_n;x_k] с шагом x. Исходные данные задать самостоятельно, в программе должно быть не менее 7-8 циклов.

Часть 1.

Программирование циклических вычислительных процессов с использованием оператора цикла For … Next.

Часть 2.

Программирование циклических вычислительных процессов с использованием оператора цикла Do … Loop с предусловием

(Do While … Loop или Do Until … Loop).

Часть 3.

Программирование циклических вычислительных процессов с использованием оператора цикла Do … Loop с постусловием

(Do … Loop Until или Do … Loop While).

Б) Выполнить вариант задания приложения 4, задание Б, с. 19.

Замечание

1) При написании программ необходимо учитывать область допустимых значений (ОДЗ).

2) Если во второй части задания А использовался оператор Do While … Loop, то в третьей части задания А лабораторной работы следует использовать оператор цикла Do…Loop Until, и наоборот.

Пример

Вычислить выражение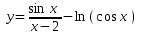

Метод разделения на части состоит в следующем: исходное выражение разбиваем на элементарные части, например:

а = sin x

b = x-2

c = cos x

После разбиения на части расчетная формула имеет следующий вид:

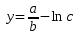
ОДЗ

b<>0, c>0

Текст программы (Часть 2, оператор цикла Do While … Loop)

Sub lr4_2()
Dim x, y, a, b, c,xn, xk, dx As Single
xn=Val(InputBox(“Введите начальное значение хn”))
xk=Val(InputBox(“Введите конечное значение хk”))
dx=Val(InputBox(“Введите шаг dx”))
x=xn
Do While x<=xk
a=sin(x)
b=x-2
c=cos(x)
If b<>0 then
If c>0 then
y=a/b-log(c)
Else
Y=“Подлогарифмическое выражение < = 0”
End If
Else
Y= “Знаменатель = 0”
End If
MsgBox “Результат Y = ” & y, , “Вывод результатов”
x=x+dx
Loop
End Sub

Контрольные вопросы

1. Оператор цикла For … Next
2. Операторы цикла Do While … Loop, Do Until … Loop
3. Операторы цикла Do … Loop While, Do … Loop Until

Варианты заданий (часть Б)

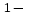
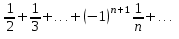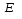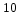
1. Найти сумму ряда S= с точностью до = 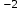. Результат печатать.

2. Вычислить cos 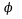( 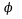- известная величина ) разложением в ряд Тейлора с точностью до = .

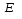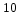
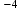3. Вычислить sin 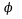( 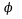- известная величина ) разложением в ряд

Тейлора с точностью до = .

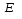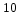
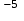4. Найти среднее арифметическое целых чисел от 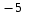до .

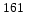5. Найти среднее арифметическое целых чисел от 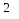до .

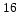6. Вычислить 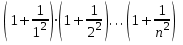для любого вводимого .

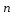7. Вычислить значение 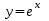при 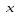= 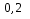разложением в ряд Тейлора с точностью до = .

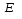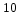
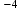8. Вычислить .

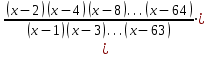9. Найти сумму ряда S= 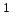+ 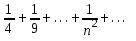с точностью до = .

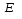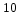
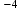10. Найти среднее геометрическое 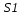всех четных чисел от 10 до 21 и среднее геометрическое 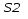всех нечетных чисел из того же интервала (в одном цикле) .

11. Найти сумму ряда S= 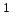+ 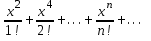с точностью до E=10 ^-4.

12. Найти сумму ряда S=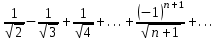 с точностью до E=10 ^-4.

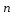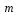13. Вычислить число сочетаний из по по формуле

С ,

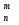
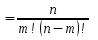где 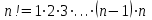, целые числа 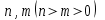ввести с клавиатуры.

14. Вычислить значение выражения

,

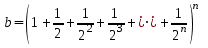где 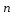ввести с клавиатуры .

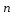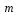15. Вычислить число размещений из по по формуле

,

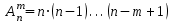где целые числа 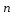и 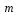ввести с клавиатуры .

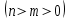16. Вычислить приближенно значение бесконечной суммы с точностью до E=10^-4

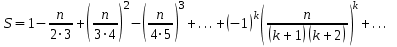
Значение 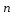и точность расчетов ввести с клавиатуры.

17. Вычислить приближенно значение бесконечной суммы с

точностью до E=10^-4

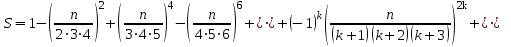
Значение 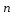и точность расчетов ввести как константы.

18. Вычислить значение функции 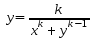для .

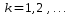Вычисления производить до тех пор , пока 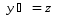. Исходные данные 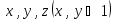ввести с клавиатуры.

19. Вычислить бесконечную сумму 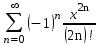с точностью до E=10^-4.

20. Вычислить бесконечную сумму 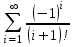с точностью до E=10 ^-4.

21. Составить программу для вычисления и вывода на экран таблицы значений сумм

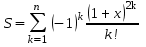
для 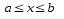, изменяющегося с шагом 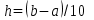. Исходные

данные :.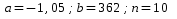

22. Переменная 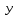изменяется от 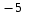до 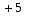включительно с шагом

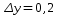. Найти наименьшее значение функции 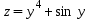на этом интервале.

23. Переменная 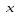изменяется с шагом 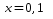на интервале 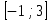. Найти наибольшее значение функции 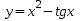для 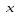, принимающих указанное значение . результат печатать .

24. Вычислить значение 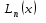многочлена Лагерра для 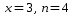по рекуррентной формуле :

.

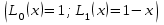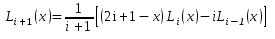
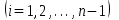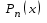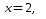
25. Вычислить значение многочлена Лежандра для 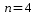по рекуррентной формуле :

.

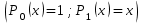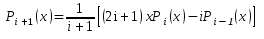
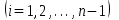26. Вычислить значение 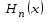многочлена Эрмита для ,

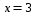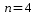по рекуррентной формуле :

.

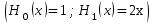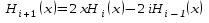
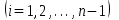27. Вычислить с точностью до 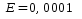значение дилогарифма для пяти значений 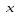по его разложению в ряд

, .

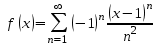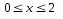28. Определить относительную погрешность вычисления факториала по формуле Стирлинга

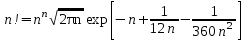
для значений .

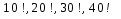29. Посчитать , сколько отрицательных значений принимает функция 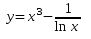, если 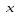изменяется от 0,25 до 3 с шагом 0,05.

. Предусмотреть случай , когда функция терпит разрыв .

30. Вычислить бесконечную сумму 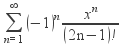с точностью до Е=10 ^-3.

CC-BY-CA Анатольев А.Г., 31.01.2012